openGauss
开源数据库
openGauss社区官网
开源社区
openGauss B-tree索引读写并发实现
openGauss B-tree 索引读写并发实现
openGauss B-tree 索引在实现时,没有完全遵循 L & Y 的理论,本文主要关注 openGauss 中 B-tree 索引的实现。
实现与理论的差异
读锁
介绍 B-tree 索引并发读写原理时讲到,L & Y 的理论中读操作完全不加锁,而是假设 B-tree 节点在内存中的拷贝是非共享的。但实际在 PG 和 openGauss 的实现中,内存中的 buffer 是共享的。所以在实现中,实际读操作需要对节点加读锁,来保证读期间没有修改操作。加锁动作降低了并发性,但保证了数据正确性。
写锁
L & Y 的理论总是将加锁和 moveright 耦合,最多同时会对三个节点加锁(分裂的子节点、父节点、父节点的右兄弟节点)。实现中,同一层的节点不需要都加锁。L & Y 的理论中通过记录从根节点开始查找路径上的节点及 key 的信息来记录父子节点关系,理论中假设所有的 key 都是不同的。实现中,父节点通过记录子节点的 Block Number 来实现父节点指向子节点的指针。理论中如果发生分裂需要更新父节点时,父节点所在层的加锁的顺序是:先对父节点加锁,如果父节点发生了分裂,则对父节点的右兄弟节点加锁,然后释放父节点的锁。而实现中,在对父节点的右兄弟节点加锁前,可以释放父节点的锁,因为 link ptr 实现中是记录的右兄弟节点的 block number, 即使右兄弟节点又发生分裂,依然可以通过 block number 找到分裂后的左侧节点,然后继续向右查找。
link ptr
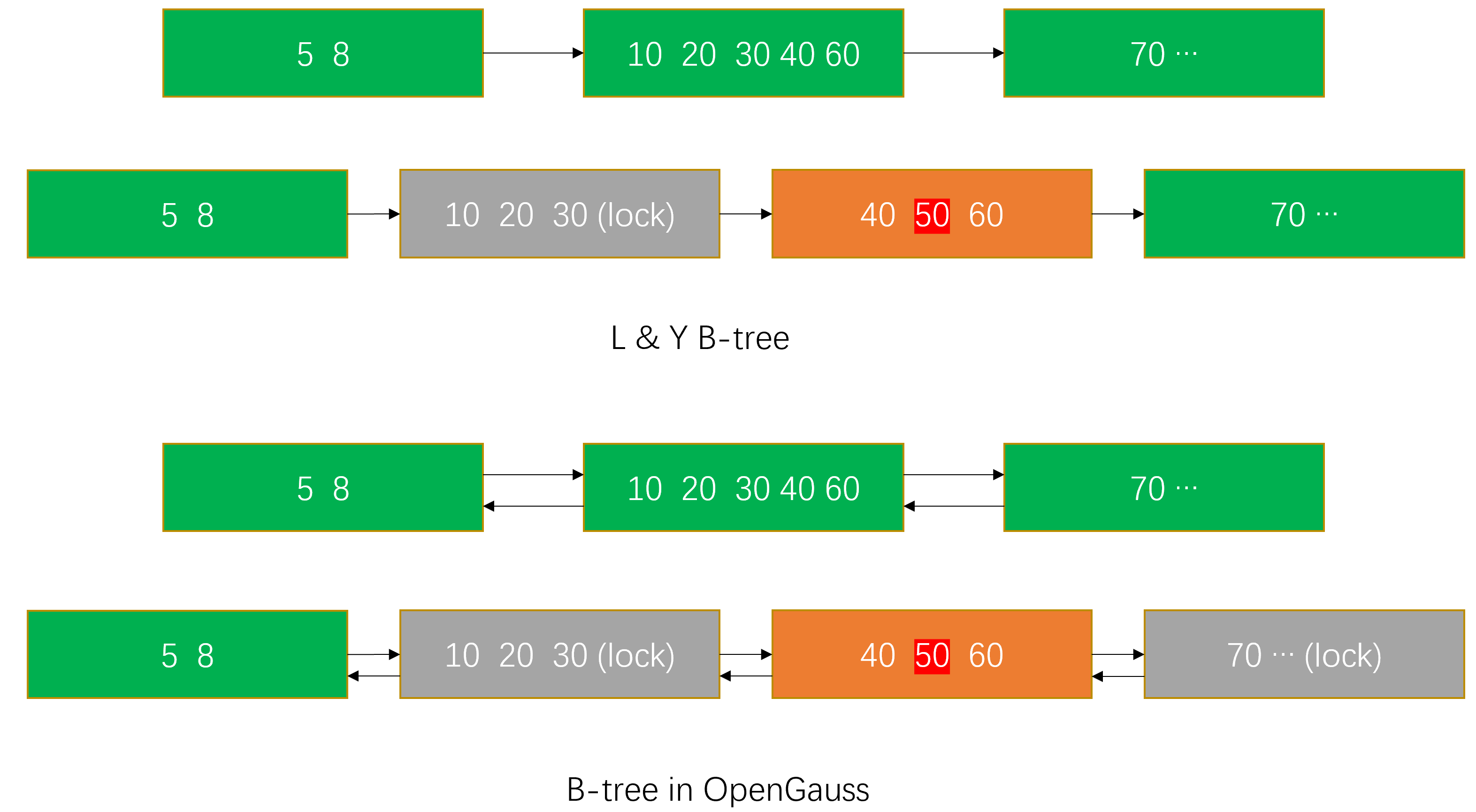
L & Y 的理论中每一层节点都有指向右侧节点的 link ptr,当执行 scan 的操作时,通过 link ptr 只能支持自左向右的 scan。为支持逆向 scan,OpenGauss 中每个节点都有指向左右两侧的两个指针,将指向同层右侧节点的称为 right link ptr,指向左侧节点的称为 left link ptr。这个修改,导致 L & Y 的理论中节点分裂需要额外的动作。在锁定分裂节点的同时,还需要锁定该节点分裂前的右兄弟,以修改其 left link ptr,如图-1 所示。实际逆向 scan 比正向 scan 要复杂一些,因为如果逆向 scan 的过程中节点发生分裂,可能还需要通过 right link ptr 向右查找(实际比更复杂,我们会在后面讨论)。
在 scan 过程中,只有在需要读一个节点时才会对其加锁,为减少加锁的时长,读操作会一次把所有满足条件的项全部读出来,在处理这些项时就可以释放锁了。有时,为了防止并发的 delete 操作,需要 pin 住某个叶子节点(后面会讲到)。scan 过程中,需要记住当前在扫描节点的 right link ptr,通过 right link ptr 向右 scan 不会遗漏数据;但如果是向左 scan,需要获取最新的 left link ptr。
大多数情况下,在对下一个节点进行 pin 和加锁前,会释放前一个节点的 pin 和锁;但有些情况下会先对下一个节点进行 pin 和加锁,再释放前一个节点的 pin 和锁。之前讲并发原理时证明过,流程中可以避免死锁的出现,但现在由于实现没有完全按照 L & Y 的理论,加了 left link ptr,似乎有死锁的可能。
L & Y 的理论中假设 key 的大小是固定的,实际需要处理变长的 key。因此对每一个 page 而言,key 的个数没有一个固定的最大值,实现中假设一个 page 内至少要有 3 个 item,因此 tuple 的大小不能超过一个 page 最大可用空间的 1/3。节点发生分裂时,按照占用空间来平均分配分裂后的左右节点,而不是按照 item 的个数均分。同时分裂需要将已经在执行中的事务占用的空间考虑在内,否则事务提交时可能出现 page 内没有足够空间的问题。
L & Y 的理论中假设 key 没有重复的,实际是对于非 unique index 可能存在重复 key。
插入
在执行数据插入的流程中,需要更新 heap tuple 和 index tuple,更新 index tuple 执行 ExecInsertIndexTuples 方法,处理的主要流程如下:
{
遍历表上的每一个索引 {
如果索引的 indisready = false,表示索引不可写,则跳过此索引;
如果是分区表的 local 索引,且 pg_partiton 中 indisusable = false,跳过此索引;
调用索引插入函数 index_insert,完成 index tuple 插入
检查索引插入是否违反约束 unique / exclusion constraint
返回结果
}
}
在介绍索引相关的代码实现之前,先介绍一下 OpenGauss 中索引实现的目录结构。
索引的实现主要在 src/gausskernel/storage/access 下,其中
- nbtree: 行存表 btree 索引的实现
- cbtree: 列存表 btree 索引的实现
- gist: gist 索引实现
- gin: 倒排索引实现
- psort: 列存表 psort 索引实现
- index: 索引对外接口
行存表支持的索引类型:btree(缺省值)、gin 和 gist。
列存表支持的索引类型:psort(缺省值)、btree 和 gin。
本文中主要介绍行存表 Btree 索引实现,对应的目录为 nbtree
index_insert
// 实现在 indexam.cpp 所有索引对外接口 { 根据索引类型,找到对应的索引插入处理函数(存储在pg_am中),例如btree索引对应的插入函数为btinsert 调用对应的插入处理函数 返回结果 }btinsert
// 实现在 nbtree.cpp,行存表btree索引插入实现 { 调用 index_form_tuple 生成 index tuple; 调用 _bt_doinsert 完成索引插入 返回结果 }_bt_doinsert
// 实现在 nbtinsert.cpp,行存表 btree 索引 index tuple 插入
{ 生成scankey用于在B-tree索引中查找插入位置。 调用 _bt_search 查找插入的叶子节点,返回一个BTStack类型的对象,该对象的实现是一个链表,链表头是叶子节点,后面的每个节点是前一个节点的父节点。由于插入数据可能导致节点分裂,子节点分裂需要更新父节点,可以通过此链表向上查找父节点。 调用 _bt_moveright,找到最终指向插入的叶子节点。因为流程不是全程加锁(先加读锁,然后释放读锁,再加写锁),因此在找到插入的叶子节点后,该节点可能由于新的插入导致分裂,则新的插入位置可能在原节点的右侧,需要向右查找(多次分裂可能需要多次向右查找);如果叶子节点没有发生变化,或者插入位置不需要向右查找,则_bt_moveright实际不做任何事情。这一点涉及Btree索引的并发控制,可以参考前一篇。 检查unique约束,包括进行中的事务,如果有执行中的事务可能导致违反约束,需要等待执行中的事务结束。 page内查找插入位置_bt_findinsertloc 执行插入操作 _bt_insertonpg }
在查找插入节点的实现 _bt_search 中,在每次使用节点时都需要调用一次 _bt_moveright ,因为查找过程中加锁的顺序是先对父节点加 ReadLock,查找到子节点(父节点指向子节点的指针的实现是记录子节点的页号)后释放父节点的 ReadLock,再对子节点加 ReadLock。由于读写并发,查找到子节点到对子节点加 ReadLock 这段时间内子节点有可能已经发生了分裂,因此在使用子节点查找时需要调用一次_bt_moveright。这样实现可以减少加锁的粒度,有利于读写并发。
_bt_search 查找到最终要执行插入的叶子节点后,在使用该节点时也要调用一次_bt_moveright,原因是查找到叶子节点后,对叶子节点加了 ReadLock。但是由于需要执行插入动作,会先释放叶子节点的 ReadLock 再对叶子节点加 WriteLock,放锁到再加锁的间隙叶子节点可能发生分裂。代码实现如下:
stack = _bt_search(rel, indnkeyatts, itup_scankey, false, &buf, BT_WRITE);
offset = InvalidOffsetNumber;
/* trade in our read lock for a write lock */
LockBuffer(buf, BUFFER_LOCK_UNLOCK);
LockBuffer(buf, BT_WRITE);
buf = _bt_moveright(rel, buf, indnkeyatts, itup_scankey, false, true, stack, BT_WRITE);
_bt_moveright
// 实现在 nbtserach.cpp 在获取到将要执行插入的叶子节点后,由于并发操作,实际位置可能发生了变化,需要由当前节点向右查找才能找到实际位置
{ 如果是写入操作insert/update,则在流程中检查是否有未完成的分裂,插入流程不允许插入一个未完成分裂中的page(通过P_INCOMPLETE_SPLIT判断。未完成的分裂可能是程序crash或者其他failure导致,special区域有标记页面的状态),因此先在流程中完成分裂动作。_bt_finish_split 这里流程的实现需要先了解 _bt_split 流程。 如果当前节点的flag是(BTP_DELETED | BTP_HALF_DEAD),表明叶子节点被删除,需要向右移动;如果当前的scan key > 节点的HK,则节点在上次获取之后发生了分裂,需要向右移动。循环检查,直到当前节点是最右节点,或者scan key <= HighKey。 }对要执行插入操作的叶子节点加锁后,需要在叶子节点内找到具体的插入位置,调用方法 _bt_findinsertloc。
_bt_findinsertloc
// 实现在 nbtinsert.cpp 在 page 内为要插入的 index tuple 查找一个插入位置(page buffer + offset)
{ 检查 tuple size 是否小于page内最大可用空间的1/3,一个page内最少要放3个tuple 如果当前page可用空间不足以放下插入的tuple,可能需要执行节点分裂。在执行分裂之前检查一下是否可以将要插入的tuple放置到右侧的某个节点中(例如 scankey = HK 的场景,可以将tuple插入右侧节点,从而避免执行分裂动作) { a. 如果是叶子节点且page内有垃圾可以清理,则调用 _bt_vacuum_one_page 做一次 page 的 vacuum,执行结束后检查 page 内的剩余空间是否足够插入tuple。 b. 如果 page-vaccum 后仍然不够或是不能执行 vacuum,检查是否满足以下两个条件: - 当前节点是最右侧节点 //不能继续向右查找 - Scan key != HK 或者 有0.99的概率向右移动 // 如果多个page内有相同的key,对查找而言可能需要不断向右查找。此时另一种选择是找一个靠左的节点将其分裂,然后有足够的空间插入要插入的tuple。这里向右继续查找的概率是0.99,有0.01的概率将当前节点分裂后进行插入。 如果当前节点处于分裂未完成的状态,先完成分裂动作 不满足 1、2两个条件,则表明 scan key = HK,则向右查找到一个有足够空间可以插入tuple的节点。 如果查找过程中向右移动了,则预期将tuple插入到节点的第一个位置(非最右节点是偏移是2,因为有HK,最右节点偏移是1)返回 对应的节点 以及 offset(入参传递); 如果没有向右移动,也没有执行vacuum,且当前的offset != INVALID,则 返回节点和offset; 其他情况需要在page内重新查找位置, 调用_bt_binsrch,返回 }上述流程由于涉及节点分裂,所以看上去有点复杂,此流程主要关注读写并发的问题,分裂后面会详述。此流程是对 page 加 WriteLock,在 page 内找到插入的位置(offset)。
找到位置后,调用 _bt_insertonpg 执行插入操作 // 实现在 nbtinsert.cpp 向page内插入一个tuple,执行时需要对buffer pin + write lock,执行完成后释放pin 和 write lock; 如果插入的节点是非叶子节点,cbuf表示插入的tuple的左子节点,插入操作会清除左子节点上的BTP_INCOMPLETE_SPLIT标记(该标记表示page处于分裂为完成的状态,通常是标记在分裂后的左侧节点上,表明分裂后父节点缺少分裂后右侧节点的信息)。 { 检查不是 incomplete split page 检查page内free space 是否足够插入 tuple,如果不够 执行分裂 调用 _bt_findsplitloc 找到分裂点,执行分裂 _bt_split,在 _bt_split 完成 tuple 的插入,完成分裂后向上更新父节点 如果空间足够,调用 _bt_pgaddtup 执行插入 执行插入的 page buffer 标脏 记Xlog }写流程中加锁顺序:
对节点加 ReadLock,获取节点信息
释放 ReadLock
加 WriteLock,执行插入操作,(可能继续执行分裂)
执行完成 Unlock
查找
_bt_search
// 实现在 nbtsearch.cpp 中,用于从B-tree的根节点开始向下查找到符合条件的叶子节点 { 获取根page _bt_getroot 调用 _bt_moveright; 如果是write-mode(插入流程查找插入位置),_bt_moveright会完成未完成的split 如果page是叶子page,则返回 否则调用 _bt_binsrch,在当前page进行查找,返回对应的item的offset。如果查找的是叶子节点,则返回的是第一个key >= scan key; 非叶子节点返回的是最后一个 key < scanKey 释放父节点的读锁,获取子节点的读锁,直到找到叶子节点。 返回一个BTStack对象(数据结构为链表,每个节点中有 block number 和 offset信息,同时还有一个指针指向父节点),如果发生分裂,可以通过此链表回溯父节点。(L&Y paper) 返回BTStack对象 }查找流程的加锁顺序:
先对父节点加 ReadLock,然后获取子节点信息,
父节点 Unlock
子节点加 ReadLock
代码如下:
{ /* drop the read lock on the parent page, acquire one on the child */ *bufP = _bt_relandgetbuf(rel, *bufP, blkno, BT_READ); ... } Buffer _bt_relandgetbuf(Relation rel, Buffer obuf, BlockNumber blkno, int access) { Buffer buf; Assert(blkno != P_NEW); if (BufferIsValid(obuf)) LockBuffer(obuf, BUFFER_LOCK_UNLOCK); buf = ReleaseAndReadBuffer(obuf, rel, blkno); LockBuffer(buf, access); _bt_checkpage(rel, buf); return buf; }
分裂
插入和查找流程都涉及节点的分裂问题,因此在这里有必要介绍一下分裂的实现。
分裂的主要实现也在 nbtinsert.cpp 中,主要逻辑在
_bt_split
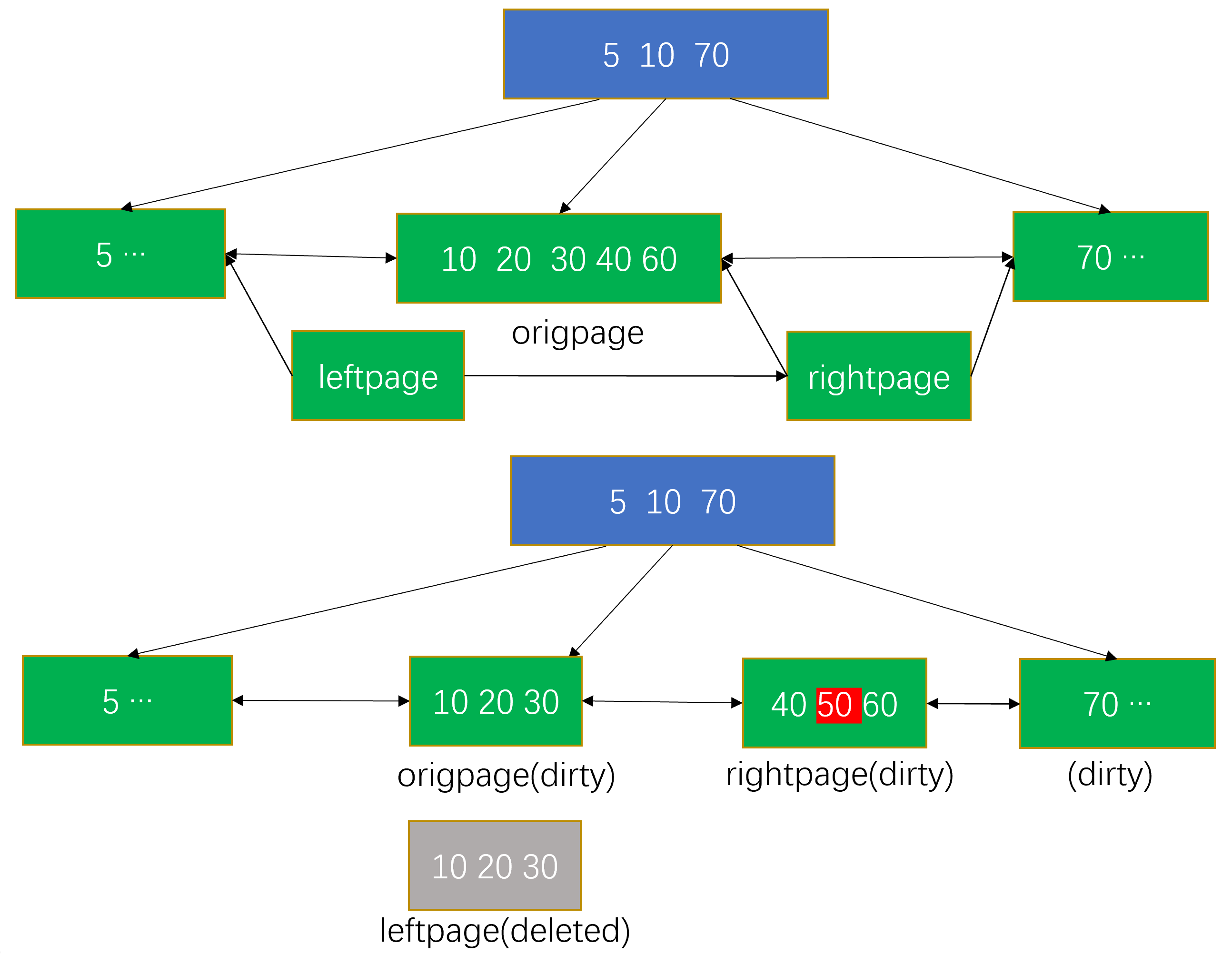
// 分裂btree中的一个节点,只实现一个page分裂为两个page,不包括更新父节点信息部分,更新父节点的实现在_bt_insert_parent { // 分裂过程中有三个 page, 原始未分裂的 page 记为 origpage,新申请的分裂后右侧的 page 记为 rightpage,临时 page 用于记录分裂后左侧节点的数据记为 leftpage,最终需要把 leftpage 拷贝回 origpage。 _bt_getbuf 申请一个新的 index page(rightpage),并对 page 进行初始化。FSM 返回一个page后,需要对这个page进行检查确保这个page没有被其他人使用。返回之前会对 page buffer 加锁以及引用计数(lock and pin)。 初始化 leftpage,拷贝 origpage 的 LSN 到 leftpage; 拷贝 origpage 中的 special pointer 中的 flags 到 leftpage ,然后设置 leftpage 中 special pointer 的 flag。将BTP_ROOT、BTP_SPLIT_END、BTP_HAS_GARBAGE三个标记位设置为0。rightpage 此标记位设置为和 leftpage 一致。 设置是 leftpage 的 special pointer 的 flag 中 BTP_INCOMPLETE_SPLIT 设置为1,表明父节点中缺少指向其右兄弟节点的指针。设置 leftpage 和 rightpage 的 link ptr。 如果分裂的节点不是最右节点,则rightpage中的第一个位置是 HighKey,否则是 user data。 确定分裂后左右两侧的数据,将数据插入左右两侧的page 对 rightpage 加 BT_WRITE 锁,用 leftpage 的内容覆盖 origpage (除了data外,special pointer 也一起更新),将 origpage 和 rightpage 的 buffer 标脏。更新原 origpage 的右兄弟节点的 left link ptr,指向rightpage,将页面标脏。 如果分裂的是非叶子节点,节点分裂完成后清除子节点上的BTP_INCOMPLETE_SPLIT标记。非叶子节点分裂是由叶子节点分裂导致,父节点完成分裂是指向表明子节点的downlink插入完成,可以将子节点的BTP_INCOMPLETE_SPLIT标记清除// 叶子节点上BTP_INCOMPLETE_SPLIT标记清除是在父节点中插入分裂后的右侧节点的指针时完成,实现是在_bt_insert_parent -> _bt_insertonpg 记XLog }
分裂过程中的加锁顺序:
origpage 加 WriteLock, 修改数据 和 right link ptr
rightpage 加 WriteLock, 修改数据 和 link ptr
origpage 分裂前的右兄弟节点加 WriteLock, 修改 left link ptr
origpage 分裂前的右兄弟节点 Unlock
rightpage Unlock
origpage Unlock
root 分裂
L & Y 的理论中没有讨论根节点分裂的问题。OpenGauss 实现时按照普通节点分裂的方式,处理根节点的分裂。根节点分裂时,需要新生成一个根节点,原来的根节点成为新根节点的子节点,根节点分裂需要额外更新 meta-page 中根节点的信息,最终结果也是正确的。
在节点分裂时,需要通过回溯的方式来更新上层节点。但如果这个上层节点是 meta-page,那么此次回溯无法正确更新,因为 meta-page 中只是元数据不能分裂。这种情况下 B-tree 产生了新的 root,需要重新走一遍查找,直到找到刚分裂的节点的上一层,然后向右查找到正确的插入位置。这通常需要重新获取 meta-page 以及新的 root-page,可以通过保存节点在 B-tree 中所处的层号(通常叶子节点是 0 层,其父节点是 1 层,以此类推),最终找到要更新的节点所处的层。
这次主要介绍了 B_tree 索引实现与理论中的一些差异点,重点介绍了读写及分裂的流程,及其中加解锁的顺序。索引数据的删除、vacuum、WAL 等内容下次再介绍。